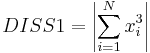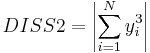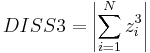...
| Descriptor name | Description |
|---|---|
| VME | molecular volume, Å3 |
| SME | molecular surface, Å2 |
| SMEP | weighted positively charged surface, 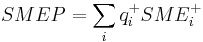 (sum for positively charged atoms; (sum for positively charged atoms; 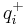 is atomic charge) is atomic charge) |
| SMEN | weighted negatively charged surface, 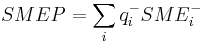 (sum for negatively charged atoms; (sum for negatively charged atoms; 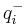 is atomic charge) is atomic charge) |
| SMED | SMEP − SMEN |
| SMEPR | fraction of positively charged area, 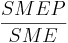 |
| SMENR | fraction of negatively charged area, 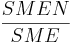 |
| SMEDR | SMEPR − SMENR |
| ESMEP | weighted average positively charged area, 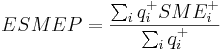 |
| ESMEN | weighted average negatively charged area, 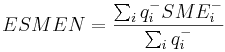 |
| ESMED | ESMEP − ESMEN |
| QSMEP | weighted average positive charge of surface, 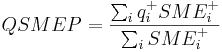 |
| QSMEN | weighted average positive charge of surface, 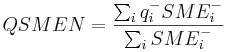 |
| QSMED | QSMEP − QSMEN |
| d204 | density of compound 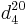 |
| DMo | dipole moment, D |
| SPH | sphericity, the ratio of surface of sphere (SS) with the volume equal to the molecular volume, and the molecular surface (SM): 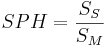 |
| VOIN1 | sum of atomic volumes, Å3 |
| VOIN1R | VOIN1R = VOIN1/VME |
| VOIN2 | sum of volumes of double overlaps of atomic spheres, Å3 |
| VOIN2R | part of double overlaps in the molecular volume, 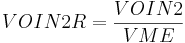 |
| VOIN3 | sum of volumes of triple overlaps of atomic spheres, Å3 |
| VOIN3R | part of triple overlaps in the molecular volume, 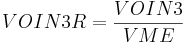 |
| VOIN4 | sum of volumes of quadruple overlaps of atomic spheres, Å3 |
| VOIN4R | part of quadruple overlaps in the molecular volume, 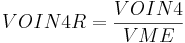 |
| VOIN5 | sum of volumes of fivefold overlaps of atomic spheres, Å3 |
| VOIN5R | part of fivefold overlaps in the molecular volume,  |
| VOIN6 | sum of volumes of sixfold overlaps of atomic spheres, Å3 |
| VOIN6R | part of sixfold overlaps in the molecular volume,  |
| HIMERA | pKA |
| MI1 | the minimal principal moment of inertia, a.u. |
| MI2 | the middle principal moment of inertia, a.u. |
| MI3 | the maximal principal moment of inertia, a.u. |
| IR1 | the minimal principal inertial radius, Å |
| IR2 | the middle principal inertial radius, Å |
| IR3 | the maximal principal inertial radius, Å |
| SI12 | the minimal principal inertial section,  , Å2 , Å2 |
| SI13 | the middle principal inertial section,  , Å2 , Å2 |
| SI23 | the maximal principal inertial section,  , Å2 , Å2 |
| PI12 | proportion of molecule in the space of principal rotational invariants, 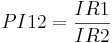 |
| PI13 | proportion of molecule in the space of principal rotational invariants, 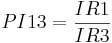 |
| PI23 | proportion of molecule in the space of principal rotational invariants, 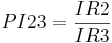 |
| DISS1 | dissymmetry about the first principal rotational invariant. The dissymmetry is calculated as the third moment (skewness), i.e. (N – number of atoms;xi is the first coordinate of ith atom in the space of principal rotational invariants), Å3 |
| DISS2 | dissymmetry about the second principal rotational invariant, (N – number of atoms; yi is the second coordinate of ith atom in the space of principal rotational invariants), Å3 |
| DISS3 | dissymmetry about the third principal rotational invariant, (N – number of atoms; zi is the third coordinate of ith atom in the space of principal rotational invariants), Å3 |
...